本相關筆記幾乎都來自於O'REILLY Deep Learning這本書籍，詳細內容有興趣的可以去網上購買。
在上一章主要講到了梯度和偏微分，這次主要解釋如何利用反向傳播求梯度。在上次使用的"數值微分"它需要計算的複雜度實在是不適合拿來訓練，但若公式先自己從答案反推回去，就能得到一個最終微分公式，雖然有誤差但其實還在接受範圍。但也存在一個問題，也就是"反向傳播"很不符合學習，因為它還需要反推才能加以順利的快速學習，不太符合人腦思考，然而也找到了關於神經網路之父所提出的反向傳播問題[1]，有興趣的人可以看一下。
接著用比較輕鬆的角度來看那些數學公式，畢竟真的要完全理解實從古代到至今的數學在是非常困難，但我們可以用自己的方式來去理解並且加以使用。數學是很抽象的但也因為抽象要理解一個東西的方法有非常多種，也是它迷人之處
。
首先從簡單的神經網路來看我們要經過輸入層->隱藏層->輸出層。
用線性方程式看神經網路，使用線性做分類只分是或不是輸出即為1或0。
二元一次線性方程式ax + by + c，在神經網路x即是神經元，a和b是權重，c是偏權值(移動量10如下圖)，輸出分為兩類等於0或小於0，因此公式為(x * w) + c若小於0則輸出0，若大於等於0輸出1。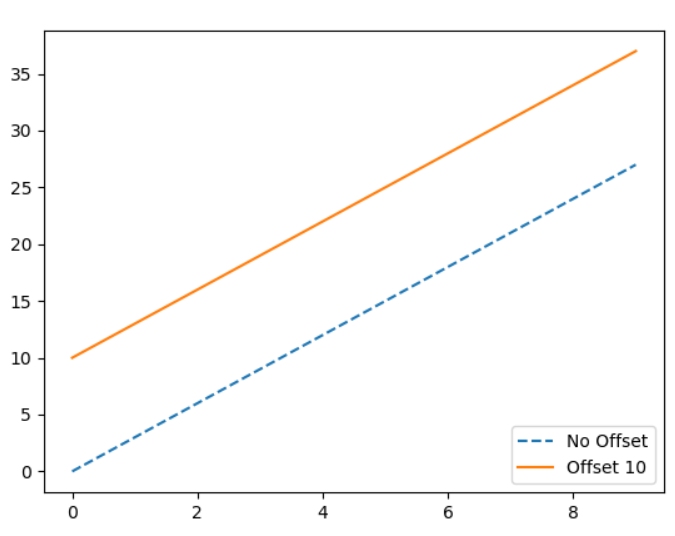
一般神經網路的輸入可能為多組向量(批量處理)，然而權重相對也是多組向量，因此在神經網路都會用下圖[3]來去表達，下方代表輸入3個向量乘上3組權重，此時就變成了矩陣相乘，這裡我們只用了一層網路，假如x是N * M的矩陣那麼W即是M * 2的矩陣，W的2是因為我們只分兩類若三類則是3已此類推，由矩陣相乘可得知N * M乘上M * 2會等於N * 2的大小，即可知道N筆資料每一筆是屬於哪一類。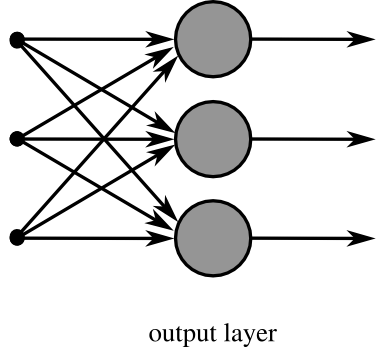
源:維基百科神經網路[2]
首先先複習一下我們上次所說的偏微分，還記得老師說過"可微分必定連續，連續卻不一定可微分"嗎，這裡介紹正規化使用的範數[4]，它是個很好的例子。什麼是範數?我把它想像是用來計算向量的長度，仔細觀察它們的公式會和距離公式(歐幾里得距離)相似，常拿來正規化或比較大小，這次介紹兩種常用範數。
範數L1: 公式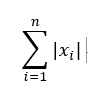
，x / x絕對值總和，例如，p1(2, 0)和p2(1, 1)的L1範數，p1範數 = 2，p2範數 = 2，使用L1正規化得到的值不是那麼的穩定，因範數L1的解容易相同，如p1.p2容易凝合若要做反向傳播(反推)時就會受影響，比較適合處理稀疏性問題。
範數L2: 公式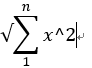
，x / x^2總和，例如，p1(2, 0)和p2(1, 1)的L1範數，p1範數 = 2，p2範數 = sqrt(2)，由範例可知L2可以解決L1凝合問題。
下圖為L1和L2比較圖，我們可以看到L2是連續平滑函數，所以可以微分，L1雖然是連續但不是平滑函數，所以不可微分(都是常數無意義)，因此在數學當中平滑函數比非平滑函數好處理許多，在機械學習也運用了許多L2範數來正規化等等。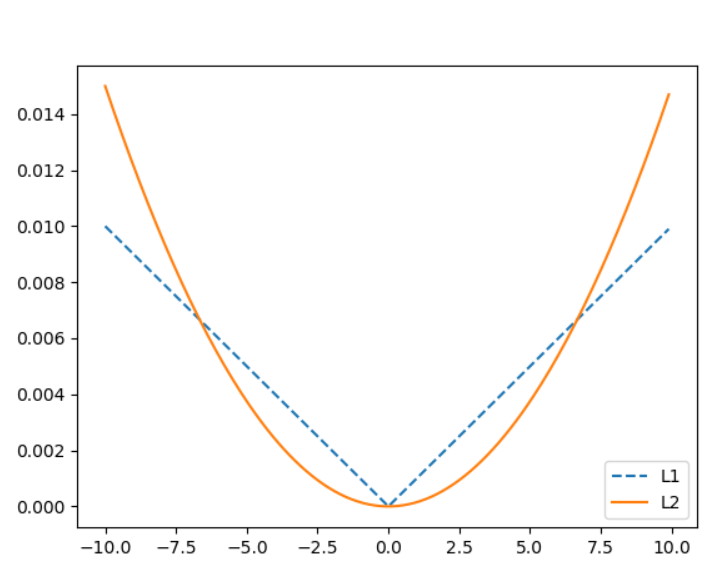
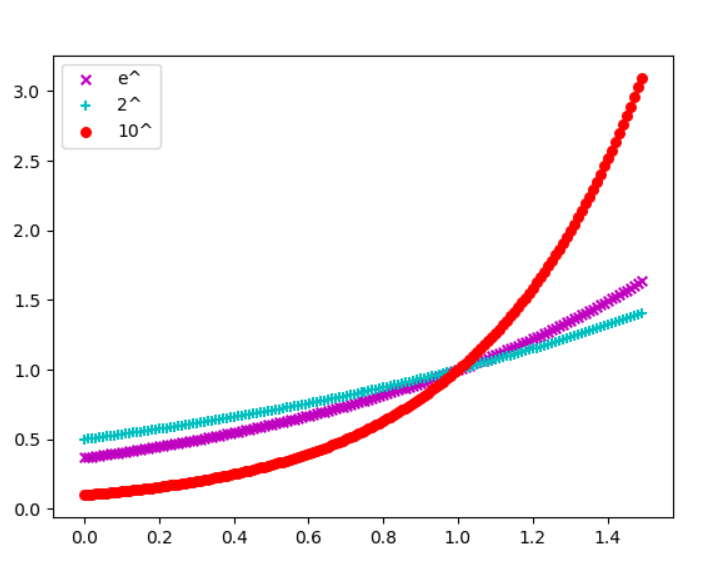
還記得在大學的微積分突然跑出個自然數e嗎?，這裡簡單介紹一下e的由來和特性為何工程上等等都會使用e。
平常使用的log就像是一張對數表，用log角度來看以2為基底如下[9]:
納皮爾想出了一個對數公式為x = b^y = (1 - 1 / 10^8)^y，我們實際計算一次如下圖[7]，它變化非常小幾乎能在這張對數表找到我們目前所需要的"小數精準對數數字"。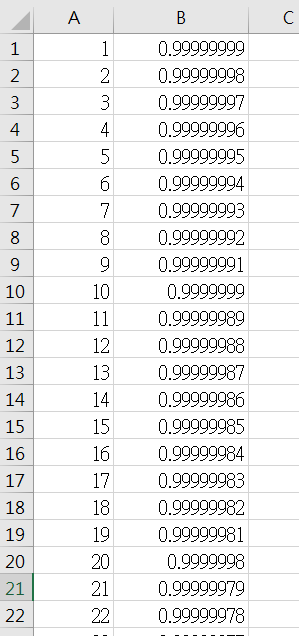
[7]
銀行在使用期數計算利息時也運用到類似的公式，例如，假設我們利率為100%(這裡設定100%，推導公式先忽略)
一年一期：金額 = 本金 * (1 + 1 / 1)
一年二期：金額 = 本金 * (1 + 1 / 2) * (1 + 1 / 2)
一年三期：金額 = 本金 * (1 + 1 / 3) * (1 + 1 / 3) * (1 + 1 / 3)
一年N期：金額 = 本金 * (1 + 1 / N)^N
上篇文章介紹的梯度，這次要將梯度拿來做訓練，上次所展示圖是計算出來的可視化梯度，然而若要訓練梯度(把梯度縮小)，它的方向就必須往內縮，可以想像上次每一個點都趨近於原點(最小位置)如下圖，最後我們訓練結果的確會很接近(0,0)，表示若有N筆資料輸入到函數(神經網路)使用梯度下降訓練係數(權重.偏權重等等)，這N筆資料最後的梯度若都是很接近的(0, 0)，那表示此函數(神經網路)可用來取的往後輸入的資料是否與目前N筆資料相似等等。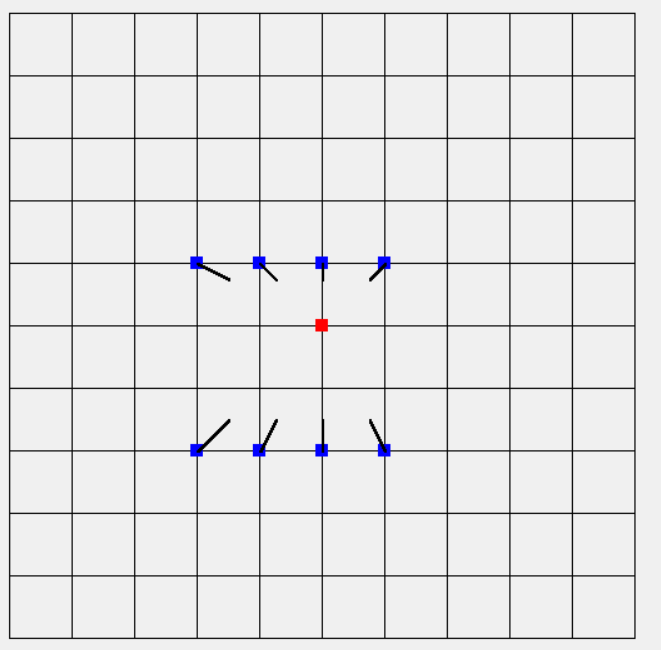
訓練時我們需要計算梯度以外還需要給它一個訓練值，訓練值主要用來控制下降大小這裡介紹幾種梯度下降公式。
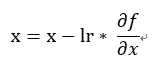，原始的x(權重) - 訓練值 * 取得x在神經網路的變化(偏微分)，但若方向原始不是只向最小值(二維平面解釋:權重差異極大導致箭頭幾乎貼近x軸或y軸)，例如歐萊里書籍提到的f(x, y)1 / 20 * x^2 + y^2 ，我們使用上次用C#來實作，多新增一個Fun2如下方程式碼取代原先的Fun1，結果如圖一，很明顯箭頭方向指向的地方差別非常大，會導致訓練必須花費更多時間甚至無法達到最好結果如圖二(也可說它不平滑)。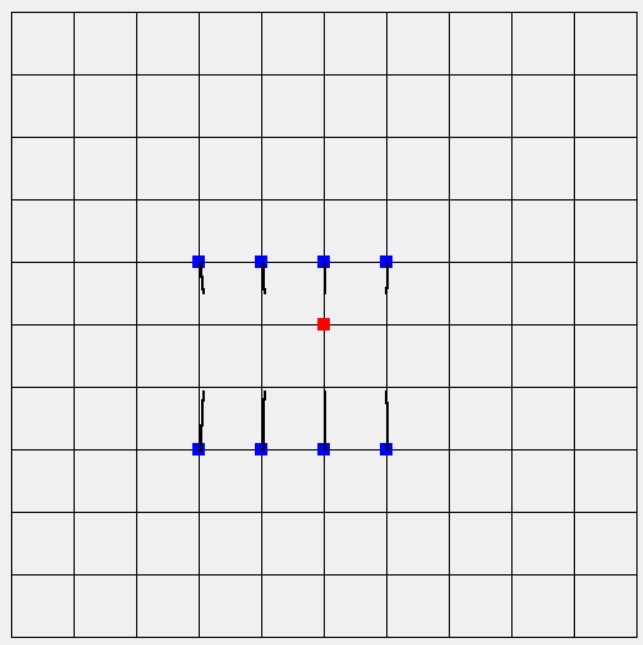
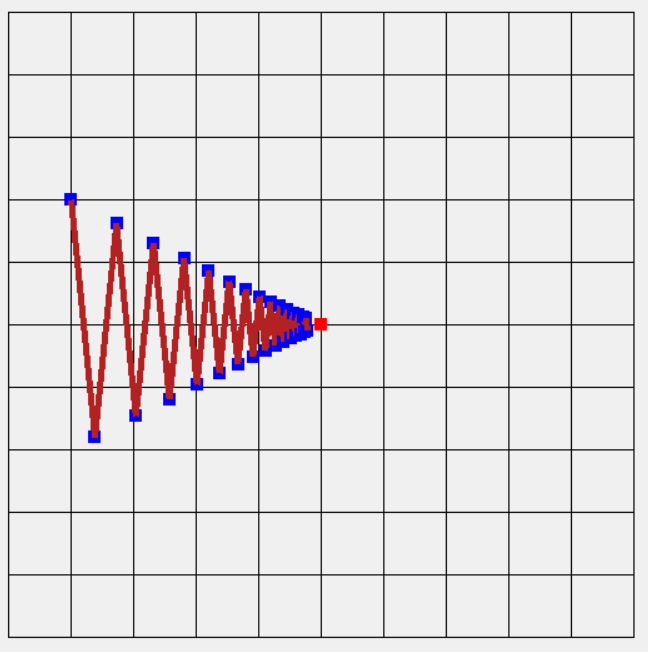
圖二
class Function2 : Function
{
public float Formula(float x, float y)
{
return x * x / 20.0f + y * y;
}
// 手動計算微分，圖二使用
public PointF2D DiffFormula(float x, float y)
{
return new PointF2D(x / 10.0f, 2.0f * y);
}
}
// 圖二使用繪製梯度下降
private void DrawSGD(Graphics graphics, DrawF draw)
{
ArrayList history = new ArrayList();
PointF2D point = new PointF2D(-4.0f, 2.0f);
Function2 fun = new Function2();
SGD optimizer = new SGD(0.95f);
for (int index = 0; index < 30; index++)
{
PointF2D xyPoint = draw.getBlockPoint(point.X, point.Y);
history.Add(xyPoint);
PointF2D diff = fun.DiffFormula(point.X, point.Y);
optimizer.Update(point, diff);
}
PointF2D prePoint = ((PointF2D)history[0]);
for (int index = 0; index < 30; index++)
{
draw.drawPoint(graphics, Brushes.Blue, ((PointF2D)history[index]));
draw.drawLine(graphics, prePoint, ((PointF2D)history[index]));
prePoint = ((PointF2D)history[index]);
}
}
// 圖二使用繪製梯度下降法函數
class SGD
{
private float _lr;
public SGD(float lr)
{
_lr = lr;
}
public void Update(PointF2D point, PointF2D grad)
{
point.X = point.X - grad.X * _lr;
point.Y = point.Y - grad.Y * _lr;
}
}
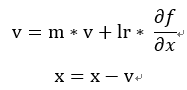，這裡主要加入了物理的摩擦力想法，多了一個m參數主要用來控制上一個動作(梯度)的摩擦力，就像你把一個東西往前推兩次，第一次向前推物體移動，若直接推第二次物體他還會加上原先的損失受力(已經在移動原先受力已經損耗)，利用這原理可讓訓練更快也讓函數更加平滑，這裡可以看出平滑函數的浮動和SGD相比差異。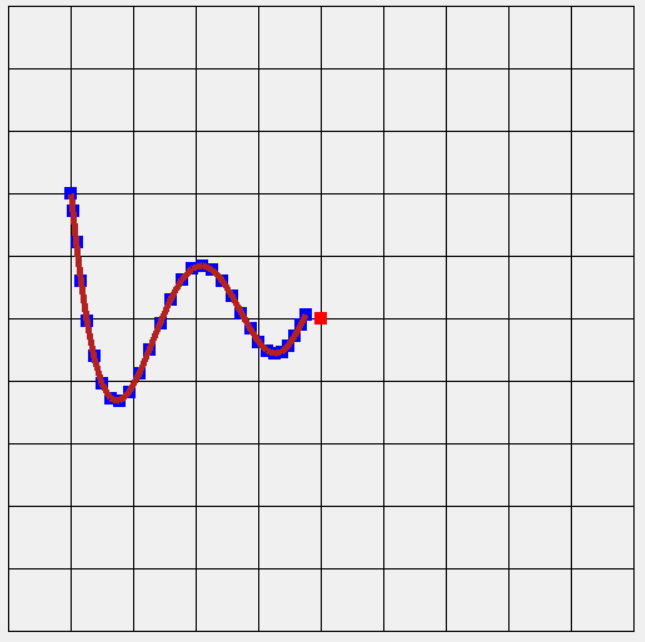
// 原本SGD只需換成Momentum
private void DrawMomentum(Graphics graphics, DrawF draw)
{
ArrayList history = new ArrayList();
PointF2D point = new PointF2D(-4.0f, 2.0f);
Function2 fun = new Function2();
Momentum optimizer = new Momentum(0.07f, 0.9f);
for (int index = 0; index < 30; index++)
{
PointF2D xyPoint = draw.getBlockPoint(point.X, point.Y);
history.Add(xyPoint);
PointF2D diff = fun.DiffFormula(point.X, point.Y);
optimizer.Update(point, diff);
}
PointF2D prePoint = ((PointF2D)history[0]);
for (int index = 0; index < 30; index++)
{
draw.drawPoint(graphics, Brushes.Blue, ((PointF2D)history[index]));
draw.drawLine(graphics, prePoint, ((PointF2D)history[index]));
prePoint = ((PointF2D)history[index]);
}
}
// Momentum函數
class Momentum
{
private float _lr;
private float _m;
private float[] _v;
public Momentum(float lr, float m)
{
_lr = lr;
_m = m;
_v = new float[2];
}
public void Update(PointF2D point, PointF2D grad)
{
_v[0] = _m * _v[0] + grad.X * _lr;
_v[1] = _m * _v[1] + grad.Y * _lr;
point.X = point.X - _v[0];
point.Y = point.Y - _v[1];
}
}
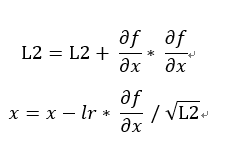，這時候就可以使用L2範化，還記得上面L2範化圖嗎，它就是利用此方法所畫出的圖形，更新到最後會趨近於0(等於0)，這方法可讓學習依L2相對的"比例"衰減，與過去梯度的平方來取得相對應的相對的比例，可看到下圖更新速度和平滑度都是不錯的。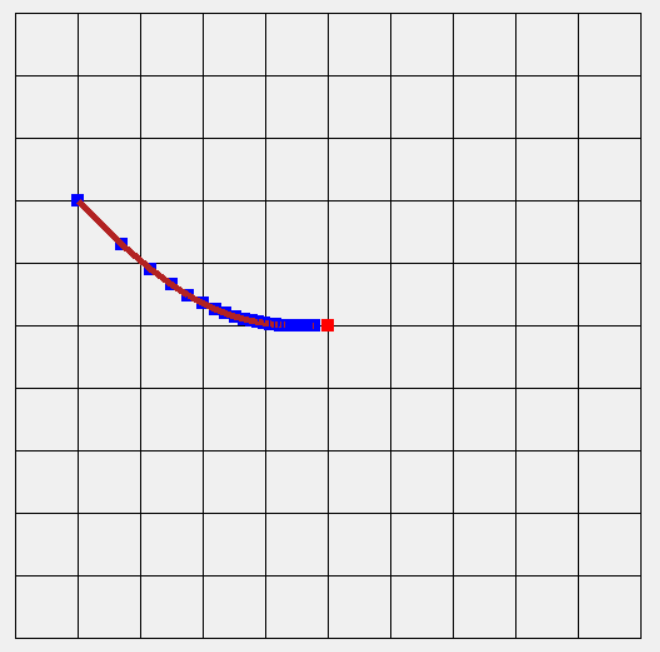
private void DrawAdaGrad(Graphics graphics, DrawF draw)
{
ArrayList history = new ArrayList();
PointF2D point = new PointF2D(-4.0f, 2.0f);
Function2 fun = new Function2();
AdaGrad optimizer = new AdaGrad(0.7f);
for (int index = 0; index < 30; index++)
{
PointF2D xyPoint = draw.getBlockPoint(point.X, point.Y);
history.Add(xyPoint);
PointF2D diff = fun.DiffFormula(point.X, point.Y);
optimizer.Update(point, diff);
}
PointF2D prePoint = ((PointF2D)history[0]);
for (int index = 0; index < 30; index++)
{
draw.drawPoint(graphics, Brushes.Blue, ((PointF2D)history[index]));
draw.drawLine(graphics, prePoint, ((PointF2D)history[index]));
prePoint = ((PointF2D)history[index]);
}
}
// AdaGrad函數
class AdaGrad
{
private float _lr;
private float[] _l2;
public AdaGrad(float lr)
{
_lr = lr;
_l2 = new float[2];
}
public void Update(PointF2D point, PointF2D grad)
{
_l2[0] = _l2[0] + grad.X * grad.X;
_l2[1] = _l2[1] + grad.Y * grad.Y;
point.X = point.X - _lr * grad.X / (float)Math.Sqrt(_l2[0] + 0.0000001f);
point.Y = point.Y - _lr * grad.Y / (float)Math.Sqrt(_l2[1] + 0.0000001f);
}
}
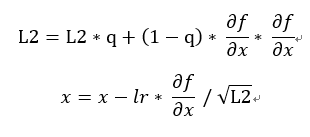，AdaGrad的改進，這裡多了一個q衰減率，每次學習都會讓過去的權重依一定比例衰減，然而就比原先AdaGrad的函數更加多變，更適合拿來處理多變函數的學習(與原先函數相比)，如下圖衰減率0.9(每次損失倍率0.1)，學習率比原先的AdaGrad還要小，點和點的間距也明顯縮小，可以讓學習更加穩定。這裡衰減率的想法就像聲波光波"傳遞"時會衰減，依人工智慧角度來看就是記憶力，會隨著時間消逝而慢慢遺忘。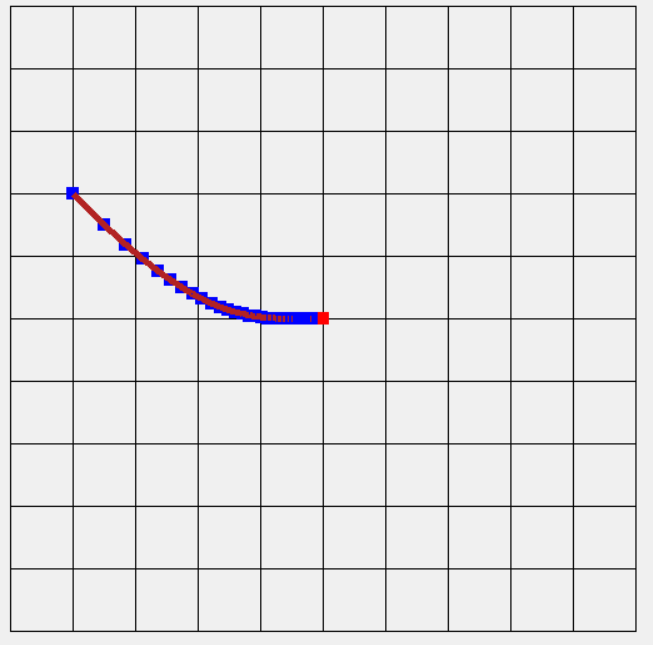
private void DrawRMSProp(Graphics graphics, DrawF draw)
{
ArrayList history = new ArrayList();
PointF2D point = new PointF2D(-4.0f, 2.0f);
Function2 fun = new Function2();
RMSProp optimizer = new RMSProp(0.5f, 0.9f);
for (int index = 0; index < 30; index++)
{
PointF2D xyPoint = draw.getBlockPoint(point.X, point.Y);
history.Add(xyPoint);
PointF2D diff = fun.DiffFormula(point.X, point.Y);
optimizer.Update(point, diff);
}
PointF2D prePoint = ((PointF2D)history[0]);
for (int index = 0; index < 30; index++)
{
draw.drawPoint(graphics, Brushes.Blue, ((PointF2D)history[index]));
draw.drawLine(graphics, prePoint, ((PointF2D)history[index]));
prePoint = ((PointF2D)history[index]);
}
}
class RMSProp
{
private float _lr;
private float _q;
private float[] _sum;
public RMSProp(float lr, float q)
{
_lr = lr;
_q = q;
_sum = new float[2];
}
public void Update(PointF2D point, PointF2D grad)
{
_sum[0] = _q * _sum[0] + grad.X * grad.X;
_sum[1] = _q * _sum[1] + grad.Y * grad.Y;
point.X = point.X - _lr * grad.X / (float)Math.Sqrt(_sum[0]);
point.Y = point.Y - _lr * grad.Y / (float)Math.Sqrt(_sum[1]);
}
}
，Adam將RMSProp和Momentum結合並計算偏差值，這裡運用到統計學計算方式未來有機會學習到在介紹真正原理。先來講解一下自己本身看法，beta1主要控制目前梯度加總的衰減率，beta2主要控制L2範數衰減率。然而這裡我們要計算偏差值，我們希望在N步前的比例是beta，近N步比例是(1 - beta)[6]，然而需要計算近N步所占的比率，當你疊代1次我們所占的比例會乘上beta，因此偏差得到beta / (1 - beta^疊代次數)，最後x減掉學習率乘上L2正規化lr * fixbeta1 / sqrt(fixbeta2)。簡單來說我們主要利用過去梯度，在計算從一開始到現在的疊代的比例，正規化後來去穩定更新梯度。
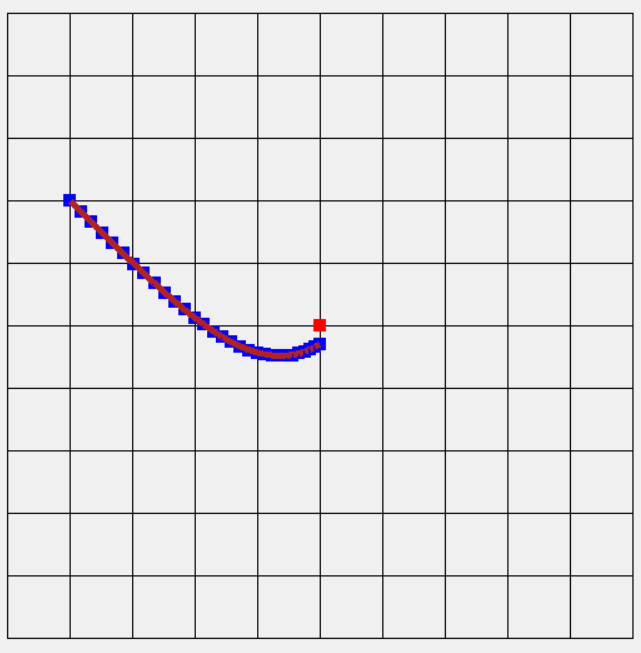
private void DrawAdam(Graphics graphics, DrawF draw)
{
ArrayList history = new ArrayList();
PointF2D point = new PointF2D(-4.0f, 2.0f);
Function2 fun = new Function2();
Adam optimizer = new Adam(0.17f, 0.9f, 0.999f);
for (int index = 0; index < 30; index++)
{
PointF2D xyPoint = draw.getBlockPoint(point.X, point.Y);
history.Add(xyPoint);
PointF2D diff = fun.DiffFormula(point.X, point.Y);
optimizer.Update(point, diff);
}
PointF2D prePoint = ((PointF2D)history[0]);
for (int index = 0; index < 30; index++)
{
draw.drawPoint(graphics, Brushes.Blue, ((PointF2D)history[index]));
draw.drawLine(graphics, prePoint, ((PointF2D)history[index]));
prePoint = ((PointF2D)history[index]);
}
}
class Adam
{
private float _lr;
private float _beta1;
private float _beta2;
private float[] _b1Sum;
private float[] _b2Sum;
private int _iter;
public Adam(float lr, float beta1, float beta2)
{
_lr = lr;
_beta1 = beta1;
_beta2 = beta2;
_b1Sum = new float[2];
_b2Sum = new float[2];
_iter = 1;
}
public void Update(PointF2D point, PointF2D grad)
{
_b1Sum[0] = _beta1 * _b1Sum[0] + (1.0f - _beta1) * grad.X;
_b1Sum[1] = _beta1 * _b1Sum[1] + (1.0f - _beta1) * grad.Y;
_b2Sum[0] = _beta2 * _b2Sum[0] + (1.0f - _beta2) * grad.X * grad.X;
_b2Sum[1] = _beta2 * _b2Sum[1] + (1.0f - _beta2) * grad.Y * grad.Y;
float[] b1Fix = new float[2];
b1Fix[0] = _b1Sum[0] / (1.0f - (float)Math.Pow(_beta1, _iter) + 0.00000001f);
b1Fix[1] = _b1Sum[1] / (1.0f - (float)Math.Pow(_beta1, _iter) + 0.00000001f);
float[] b2Fix = new float[2];
b2Fix[0] = _b2Sum[0] / (1.0f - (float)Math.Pow(_beta2, _iter) + 0.00000001f);
b2Fix[1] = _b2Sum[1] / (1.0f - (float)Math.Pow(_beta2, _iter) + 0.00000001f);
point.X = point.X - _lr * b1Fix[0] / ((float)Math.Sqrt(b2Fix[0]) + 0.00000001f);
point.Y = point.Y - _lr * b1Fix[1] / ((float)Math.Sqrt(b2Fix[1]) + 0.00000001f);
_iter++;
}
}
上述所說的輸出0或1是就是屬於活化函數的其中一種(階梯函數)，活化函數主要是用來分界，然而活化函數有非常多種，在這裡主要介紹其中的兩種，這裡做大概介紹。
Sigmoid函數:公式為1 / (1 + exp(-x))，主要分布於0 ~ 1但到某個值(好像是4.X和-4.X)會非常趨近1和0。這時候超過某個值都會是相同的，也就是我們會失去一些原先的訊息。
Relu函數:公式為x < 0輸出0，x > 0輸出x，主要分布0~N，把小於0的值都設定為0，大於直接輸出。但這時候我們將會失去負號的相關資訊，然而就有人提出進階的Relu想法(合併Sigmoid函數等等)。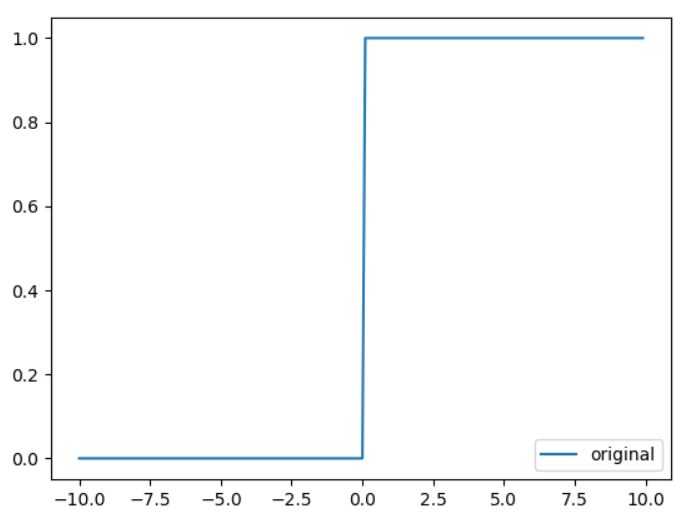
階梯函數
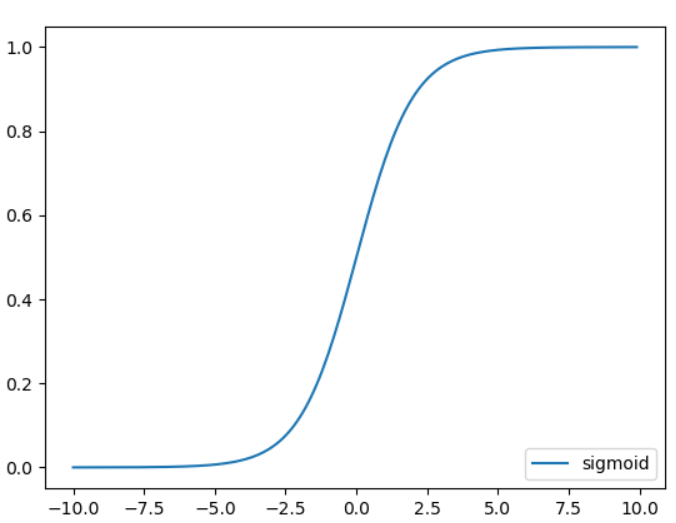
Sigmoid
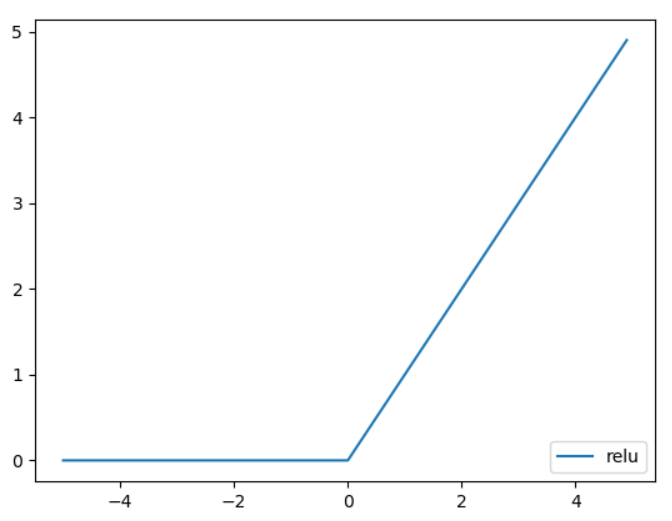
Relu
然而使用這裡使用Relu函數或Sigmoid函數來取代階梯函數，他們保留的資訊比階梯函數多，往後才能取得梯度，比較不會導致梯度消失(原始資訊消失)，資訊流失少我們取梯地做反向傳播資料也會比較正確。
當資料處理完，選擇我們解決的問題所需函數。輸出層函數的選擇分為兩種，第一回歸問題(預測數值)，第二分類問題(分類機率)。
損失函數主要是拿來與我們"現在已有的正確答案"來做比對，會依據損失函數來去判斷輸出的分類結果和正確答案的誤差，這時候你會想到前面介紹的範數，使2個向量去做比較，以下介紹兩種損失函數。
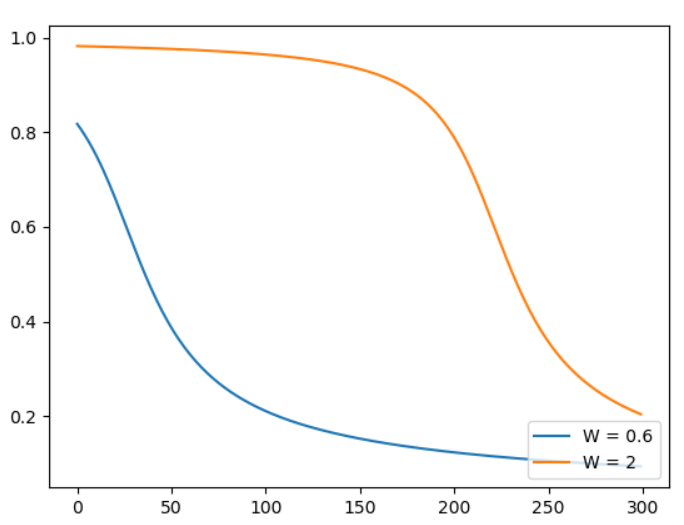
公式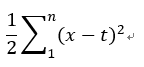
，我們把它當作再算兩點距離相加，1 / 2似乎是因為方便微分可有可無。參考此文章，首先我們先使用簡單的方式來更新，我們將前面結合起來 輸入神經元 -> * 權重 + 偏權重 -> softmax正規化 -> 均方誤差比較 -> 取得誤差梯度 -> 更新梯度(這裡使用SGD)，疊代300次。假設一權重 = 0.6.偏權重 = 0.9，假設二權重 = 2，偏權重 = 2 [6]。疊代300次結果如下圖，可以看到假設二剛開始更新很慢，不穩定這就是均方誤差更新的缺點。
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def fun(x, w, b):
return x * w + b
def loss(x, w, b):
a = fun(x, w, b)
y = sigmoid(a)
return 0.5 * (y ** 2)
def get_grad(x, w, b):
h = 1e-2
grad = {}
temp = w
w = temp + h
fun1 = loss(x, w, b)
w = temp - h
fun2 = loss(x, w, b)
w = temp
grad['dW'] = (fun1 - fun2) / (2 * h)
temp = b
b = temp + h
fun1 = loss(x, w, b)
b = temp - h
fun2 = loss(x, w, b)
b = temp
grad['db'] = (fun1 - fun2) / (2 * h)
return grad
def tran(x, w, b):
lr = 0.15
times = 300
history_y = []
for index in range(300):
a = fun(x, w, b)
y = sigmoid(a)
history_y.append(y)
grad = get_grad(x, w, b)
w -= lr * grad['dW']
b -= lr * grad['db']
return history_y
if __name__ == '__main__':
y1 = tran(1, 0.6, 0.9)
y2 = tran(1, 2, 2)
plt.plot(np.arange(0, 300, 1), np.array(y1), label = 'W = 0.6')
plt.plot(np.arange(0, 300, 1), np.array(y2), label = 'W = 2')
plt.legend()
plt.show()
公式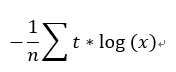
，利用統計學的交叉熵來去取得目前的誤差，以下介紹信息熵。直觀角度觀看就是在計算A的信息量乘上所佔的B的比例，也就是當算出來結果熵越高代表信息越多(也能說獲得的利益越大)。
信息熵(無二類)
在統計學中的信息熵公式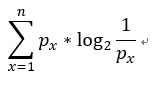
，它主要是計算每個訊息估計需要拿取幾次才能得到，參考[11]的題目我們這裡用二元樹分析。
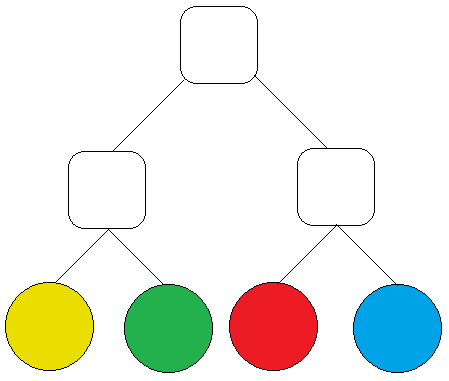
假設一：有四顆球分別為黃色.綠色.紅色.藍色比率均為1 / 4，使用用二元樹來分析它的信息熵如下圖1，在二元樹當中每一層只有分拿與不拿兩種可能，走一層算拿一次(Root下去算第一層)。
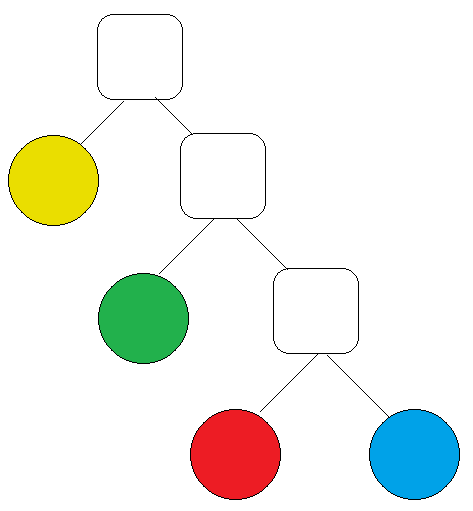
假設二：有四顆球分別為黃色有1 / 2.綠色有1 / 4.紅色有1 / 8.藍色有1 / 8，使用用二元樹來分析它的信息熵如下圖2，在二元樹當中每一層只有分拿與不拿兩種可能，走一層算拿一次(Root下去算第一層)。
交叉熵
交叉摘公式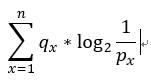
，你會發現與信息熵差了一個q，沒錯其實它們是一樣的只是當我們今天要比對哪個信息(拿的次數)更符合我們現在的q，信息越小代表越好。
例如我們把剛剛假設二的次數更換為假設一，交叉熵 = 1 / 2 * 2 + 1 / 4 * 2 + 1 / 8 * 2 + 1 / 8 * 2 = 2，比原本的1.75還大，代表著原本的拿取方式更加準確。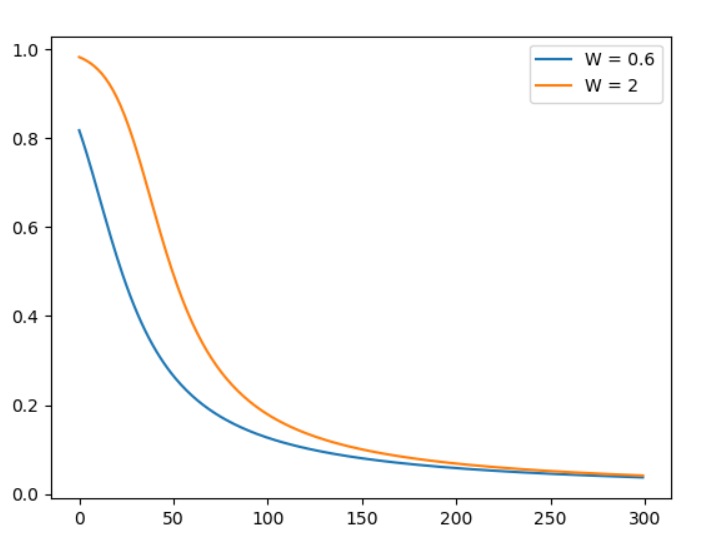
# 取代平均方差，這裡我們測試，只有一個答案，所以用原來的交叉熵公式
def loss(x, w, b):
a = fun(x, w, b)
y = sigmoid(a)
return -np.sum(0 * np.log(y) + (1 - 0) * np.log((1 - y) + 1e-7))
原來的交叉熵公式只有分兩類，所以當輸出答案是0或1就代表已經訓練完成，所以才需要多計算(1 - 正確答案)防止遇到0情況，本例題就是0，但通常我們我們訓練都會使用上述公式。
在程式上面我們使用的log為e若不清楚為何要用e可往上看，然而這裡比較不同的地方是多了-1 / n，n是為了計算批量，而負號在這裡的解釋為"差多少"(我少1所以要加1的意思)，而不是"誤差多少"。
人工智慧運用了線代.離散.統計...等等，要學的東西真的是滿多的，老師當時在教的時候只會算卻不知道它能做甚麼，使用了才發現這些要去理解它在做甚麼"用途"，也不用特地背公式，當然能背起來最好，最後一年大學希望能增加自己能力也希望推甄可以進。
這次文章寫了有一點久，原先想把反向傳播和優化等等全部加進去，但似乎只能放到下一次文章了。這次記錄這些筆記主要將數學公式敘述成自己想法，然而可以自行創造新的公式，但有的可能想法有誤，將來學到正確的想法還會再更新錯誤的想法，若有錯誤麻煩糾正，祝大家假日愉快
。
[1]https://kknews.cc/science/b4l89a6.html
[2]https://zh.wikipedia.org/wiki/%E4%BA%BA%E5%B7%A5%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
[3]https://zh.wikipedia.org/wiki/Softmax%E5%87%BD%E6%95%B0
[4]https://www.jianshu.com/p/de05e6745fb6
[5]http://www.voidcn.com/article/p-sazgzwbp-cc.html
[6]https://hit-scir.gitbooks.io/neural-networks-and-deep-learning-zh_cn/content/chap3/c3s1.html
[7]http://otherchang.pixnet.net/blog/post/31904616-%E8%87%AA%E7%84%B6%E5%BA%95%E6%95%B8-e-%E7%9A%84%E5%AE%9A%E7%BE%A9-%28%E4%B8%8A%29
[8]https://zh.wikipedia.org/wiki/E_(%E6%95%B0%E5%AD%A6%E5%B8%B8%E6%95%B0)
[9]http://blog.udn.com/cchahacaptain/4565752
[10]https://stats.stackexchange.com/questions/27682/what-is-the-reason-why-we-use-natural-logarithm-ln-rather-than-log-to-base-10
[11]https://www.zhihu.com/question/41252833
感謝大大分享，內容超級豐富，不過我數學不好讀起來有點吃力，
過陣子有空再來補充深度學習的知識，
您的 Cubic UFO 不明立體飛行物，我還在研究中呢，哈哈哈。
數學很抽象需要想像力，可以看參考網址想出自己的方式比較適合自己。
那題重點大概是旋轉矩陣和找凸型點在二分法算面積，但題目給的座標不是(0, 0, 0)而是中心(0.5, 0.5, 0.5)我也是上網找三維座標相關才知道它說的中心點意思哈哈。
了解，對於數學我要學的還很多，看您將數學公式畫成曲線圖就覺得很厲害。
看圖形比較好理解, 我數學也爛爛的還在努力
iThome鐵人賽
看影片追技術